Draw This Tree to Be Balanced
How to determine if a binary tree is height-balanced?
A tree where no leaf is much farther away from the root than any other leaf. Different balancing schemes allow different definitions of "much farther" and different amounts of work to keep them balanced.
Consider a height-balancing scheme where following conditions should be checked to determine if a binary tree is balanced.
An empty tree is height-balanced. A non-empty binary tree T is balanced if:
1) Left subtree of T is balanced
2) Right subtree of T is balanced
3) The difference between heights of left subtree and right subtree is not more than 1.
The above height-balancing scheme is used in AVL trees. The diagram below shows two trees, one of them is height-balanced and other is not. The second tree is not height-balanced because height of left subtree is 2 more than height of right subtree.
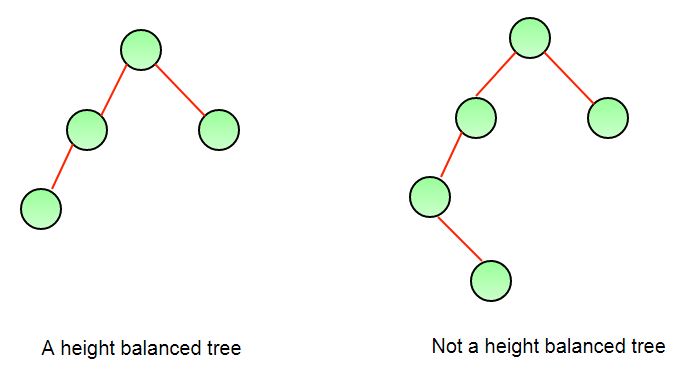
To check if a tree is height-balanced, get the height of left and right subtrees. Return true if difference between heights is not more than 1 and left and right subtrees are balanced, otherwise return false.
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public :
int data;
node* left;
node* right;
};
int height(node* node);
bool isBalanced(node* root)
{
int lh;
int rh;
if (root == NULL)
return 1;
lh = height(root->left);
rh = height(root->right);
if ( abs (lh - rh) <= 1 && isBalanced(root->left) && isBalanced(root->right))
return 1;
return 0;
}
int max( int a, int b)
{
return (a >= b) ? a : b;
}
int height(node* node)
{
if (node == NULL)
return 0;
return 1 + max(height(node->left),
height(node->right));
}
node* newNode( int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
int main()
{
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->left->left->left = newNode(8);
if (isBalanced(root))
cout << "Tree is balanced" ;
else
cout << "Tree is not balanced" ;
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
#define bool int
struct node {
int data;
struct node* left;
struct node* right;
};
int height( struct node* node);
bool isBalanced( struct node* root)
{
int lh;
int rh;
if (root == NULL)
return 1;
lh = height(root->left);
rh = height(root->right);
if ( abs (lh - rh) <= 1 && isBalanced(root->left) && isBalanced(root->right))
return 1;
return 0;
}
int max( int a, int b)
{
return (a >= b) ? a : b;
}
int height( struct node* node)
{
if (node == NULL)
return 0;
return 1 + max(height(node->left), height(node->right));
}
struct node* newNode( int data)
{
struct node* node = ( struct node*)
malloc ( sizeof ( struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->left->left->left = newNode(8);
if (isBalanced(root))
printf ( "Tree is balanced" );
else
printf ( "Tree is not balanced" );
getchar ();
return 0;
}
Java
class Node {
int data;
Node left, right;
Node( int d)
{
data = d;
left = right = null ;
}
}
class BinaryTree {
Node root;
boolean isBalanced(Node node)
{
int lh;
int rh;
if (node == null )
return true ;
lh = height(node.left);
rh = height(node.right);
if (Math.abs(lh - rh) <= 1
&& isBalanced(node.left)
&& isBalanced(node.right))
return true ;
return false ;
}
int height(Node node)
{
if (node == null )
return 0 ;
return 1 + Math.max(height(node.left), height(node.right));
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node( 1 );
tree.root.left = new Node( 2 );
tree.root.right = new Node( 3 );
tree.root.left.left = new Node( 4 );
tree.root.left.right = new Node( 5 );
tree.root.left.left.left = new Node( 8 );
if (tree.isBalanced(tree.root))
System.out.println( "Tree is balanced" );
else
System.out.println( "Tree is not balanced" );
}
}
Python3
class Node:
def __init__( self , data):
self .data = data
self .left = None
self .right = None
def height(root):
if root is None :
return 0
return max (height(root.left), height(root.right)) + 1
def isBalanced(root):
if root is None :
return True
lh = height(root.left)
rh = height(root.right)
if ( abs (lh - rh) < = 1 ) and isBalanced(
root.left) is True and isBalanced( root.right) is True :
return True
return False
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( 3 )
root.left.left = Node( 4 )
root.left.right = Node( 5 )
root.left.left.left = Node( 8 )
if isBalanced(root):
print ( "Tree is balanced" )
else :
print ( "Tree is not balanced" )
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node( int d)
{
data = d;
left = right = null ;
}
}
public class BinaryTree {
public Node root;
public virtual bool isBalanced(Node node)
{
int lh;
int rh;
if (node == null ) {
return true ;
}
lh = height(node.left);
rh = height(node.right);
if (Math.Abs(lh - rh) <= 1 && isBalanced(node.left)
&& isBalanced(node.right)) {
return true ;
}
return false ;
}
public virtual int height(Node node)
{
if (node == null ) {
return 0;
}
return 1 + Math.Max(height(node.left), height(node.right));
}
public static void Main( string [] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.left.left.left = new Node(8);
if (tree.isBalanced(tree.root)) {
Console.WriteLine( "Tree is balanced" );
}
else {
Console.WriteLine( "Tree is not balanced" );
}
}
}
Javascript
<script>
class Node{
constructor(data){
this .data = data
this .left = null
this .right = null
}
}
function height(root){
if (root == null )
return 0
return Math.max(height(root.left), height(root.right)) + 1
}
function isBalanced(root){
if (root == null )
return true
let lh = height(root.left)
let rh = height(root.right)
if (Math.abs(lh - rh) <= 1 && isBalanced(
root.left)== true && isBalanced( root.right) == true )
return true
return false
}
let root = new Node(1)
root.left = new Node(2)
root.right = new Node(3)
root.left.left = new Node(4)
root.left.right = new Node(5)
root.left.left.left = new Node(8)
if (isBalanced(root))
document.write( "Tree is balanced" , "</br>" )
else
document.write( "Tree is not balanced" , "</br>" )
</script>
Output:
Tree is not balanced
Time Complexity: O(n^2) in case of full binary tree.
Optimized implementation: Above implementation can be optimized by calculating the height in the same recursion rather than calling a height() function separately. Thanks to Amar for suggesting this optimized version. This optimization reduces time complexity to O(n).
C++
#include <bits/stdc++.h>
using namespace std;
#define bool int
class node {
public :
int data;
node* left;
node* right;
};
bool isBalanced(node* root, int * height)
{
int lh = 0, rh = 0;
int l = 0, r = 0;
if (root == NULL) {
*height = 0;
return 1;
}
l = isBalanced(root->left, &lh);
r = isBalanced(root->right, &rh);
*height = (lh > rh ? lh : rh) + 1;
if ( abs (lh - rh) >= 2)
return 0;
else
return l && r;
}
node* newNode( int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
int main()
{
int height = 0;
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->left->left->left = newNode(7);
if (isBalanced(root, &height))
cout << "Tree is balanced" ;
else
cout << "Tree is not balanced" ;
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
#define bool int
struct node {
int data;
struct node* left;
struct node* right;
};
bool isBalanced( struct node* root, int * height)
{
int lh = 0, rh = 0;
int l = 0, r = 0;
if (root == NULL) {
*height = 0;
return 1;
}
l = isBalanced(root->left, &lh);
r = isBalanced(root->right, &rh);
*height = (lh > rh ? lh : rh) + 1;
if ( abs (lh - rh) >= 2)
return 0;
else
return l && r;
}
struct node* newNode( int data)
{
struct node* node = ( struct node*)
malloc ( sizeof ( struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
int height = 0;
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->left->left->left = newNode(7);
if (isBalanced(root, &height))
printf ( "Tree is balanced" );
else
printf ( "Tree is not balanced" );
getchar ();
return 0;
}
Java
class Node {
int data;
Node left, right;
Node( int d)
{
data = d;
left = right = null ;
}
}
class Height {
int height = 0 ;
}
class BinaryTree {
Node root;
boolean isBalanced(Node root, Height height)
{
if (root == null ) {
height.height = 0 ;
return true ;
}
Height lheight = new Height(), rheight = new Height();
boolean l = isBalanced(root.left, lheight);
boolean r = isBalanced(root.right, rheight);
int lh = lheight.height, rh = rheight.height;
height.height = (lh > rh ? lh : rh) + 1 ;
if (Math.abs(lh - rh) >= 2 )
return false ;
else
return l && r;
}
public static void main(String args[])
{
Height height = new Height();
BinaryTree tree = new BinaryTree();
tree.root = new Node( 1 );
tree.root.left = new Node( 2 );
tree.root.right = new Node( 3 );
tree.root.left.left = new Node( 4 );
tree.root.left.right = new Node( 5 );
tree.root.right.right = new Node( 6 );
tree.root.left.left.left = new Node( 7 );
if (tree.isBalanced(tree.root, height))
System.out.println( "Tree is balanced" );
else
System.out.println( "Tree is not balanced" );
}
}
Python3
class Node:
def __init__( self , data):
self .data = data
self .left = self .right = None
class Height:
def __init__( self ):
self .height = 0
def height(root):
if root is None :
return 0
return max (height(root.left), height(root.right)) + 1
def isBalanced(root):
if root is None :
return True
lh = Height()
rh = Height()
lh.height = height(root.left)
rh.height = height(root.right)
l = isBalanced(root.left)
r = isBalanced(root.right)
if abs (lh.height - rh.height) < = 1 :
return l and r
return False
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( 3 )
root.left.left = Node( 4 )
root.left.right = Node( 5 )
root.right.left = Node( 6 )
root.left.left.left = Node( 7 )
if isBalanced(root):
print ( 'Tree is balanced' )
else :
print ( 'Tree is not balanced' )
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node( int d)
{
data = d;
left = right = null ;
}
}
public class Height {
public int height = 0;
}
public class BinaryTree {
public Node root;
public virtual bool isBalanced(Node root, Height height)
{
if (root == null ) {
height.height = 0;
return true ;
}
Height lheight = new Height(), rheight = new Height();
bool l = isBalanced(root.left, lheight);
bool r = isBalanced(root.right, rheight);
int lh = lheight.height, rh = rheight.height;
height.height = (lh > rh ? lh : rh) + 1;
if (Math.Abs(lh - rh) >= 2) {
return false ;
}
else {
return l && r;
}
}
public virtual int height(Node node)
{
if (node == null ) {
return 0;
}
return 1 + Math.Max(height(node.left), height(node.right));
}
public static void Main( string [] args)
{
Height height = new Height();
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.right = new Node(6);
tree.root.left.left.left = new Node(7);
if (tree.isBalanced(tree.root, height)) {
Console.WriteLine( "Tree is balanced" );
}
else {
Console.WriteLine( "Tree is not balanced" );
}
}
}
Javascript
<script>
class Node{
constructor(data){
this .data = data
this .left = this .right = null
}
}
class Height
{
constructor()
{
this .height = 0
}
}
function height(root){
if (root == null )
return 0
return Math.max(height(root.left), height(root.right)) + 1
}
function isBalanced(root)
{
if (root == null )
return true
let lh = new Height()
let rh = new Height()
lh.height = height(root.left)
rh.height = height(root.right)
let l = isBalanced(root.left)
let r = isBalanced(root.right)
if (Math.abs(lh.height - rh.height) <= 1)
return l && r
return false
}
let root = new Node(1)
root.left = new Node(2)
root.right = new Node(3)
root.left.left = new Node(4)
root.left.right = new Node(5)
root.right.left = new Node(6)
root.left.left.left = new Node(7)
if (isBalanced(root))
document.write( 'Tree is balanced' , "</br>" )
else
document.write( 'Tree is not balanced' , "</br>" )
</script>
Output
Tree is balanced
Time Complexity: O(n)
Auxiliary Space: O(n)
Please write comments if you find any of the above codes/algorithms incorrect, or find other ways to solve the same problem.
Source: https://www.geeksforgeeks.org/how-to-determine-if-a-binary-tree-is-balanced/
0 Response to "Draw This Tree to Be Balanced"
Post a Comment